標準偏差 (Standard Deviation) | Webクローラ | ScrapeStorm
摘要:標準偏差は、データのばらつきや散らばり具合を表す統計量です。具体的には、データの各値が平均値からどれだけ離れているかを測定する指標であり、データセット内のばらつきの大きさを数値で示します。標準偏差が小さいほどデータは平均値に集中しており、大きいほどデータが広がっていることを意味します。 ScrapeStorm無料ダウンロード
ScrapeStormとは、強い機能を持つ、プログラミングが必要なく、使いやすい人工知能Webスクレイピングツールです。
概要
標準偏差は、データのばらつきや散らばり具合を表す統計量です。具体的には、データの各値が平均値からどれだけ離れているかを測定する指標であり、データセット内のばらつきの大きさを数値で示します。標準偏差が小さいほどデータは平均値に集中しており、大きいほどデータが広がっていることを意味します。
標準偏差の計算方法は、まずデータセットの平均を求め、その後各データ値から平均を引き、その差を二乗して平均を取ります。最後に、その平均の平方根を取ることで標準偏差を得ます。
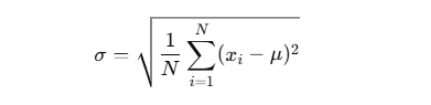
適用シーン
株式市場や投資において、標準偏差はリスクの指標として使われます。株価の変動幅を測ることで、投資のリスクの大きさを理解することができます。製造業では、製品の品質のばらつきを評価するために標準偏差が使用されます。生産ラインでの製品の均一性を確認するために重要です。テストの点数や成績分布を分析する際に、標準偏差を使って学生の成績のばらつき具合を評価することができます。
メリット:標準偏差はデータのばらつき具合を直接的に示すため、データの分布を理解しやすいです。標準偏差は比較的簡単に計算できるため、統計分析で広く使用されています。標準偏差は様々な分野で使用される汎用的な指標であり、特にデータの分布の形を知る上で重要です。
デメリット:標準偏差は外れ値(異常値)に敏感です。外れ値がデータに含まれると、標準偏差が大きくなる可能性があり、実際のばらつき具合を正確に反映しないことがあります。標準偏差は正規分布において最も有効に機能しますが、他の分布(例えば、偏った分布や非対称な分布)においてはその解釈が難しくなることがあります。標準偏差は元のデータの単位に依存します。例えば、距離を測定するデータに対して標準偏差を計算すると、結果も距離の単位で表されますが、他の単位で表すとその解釈が難しくなることがあります。
図例
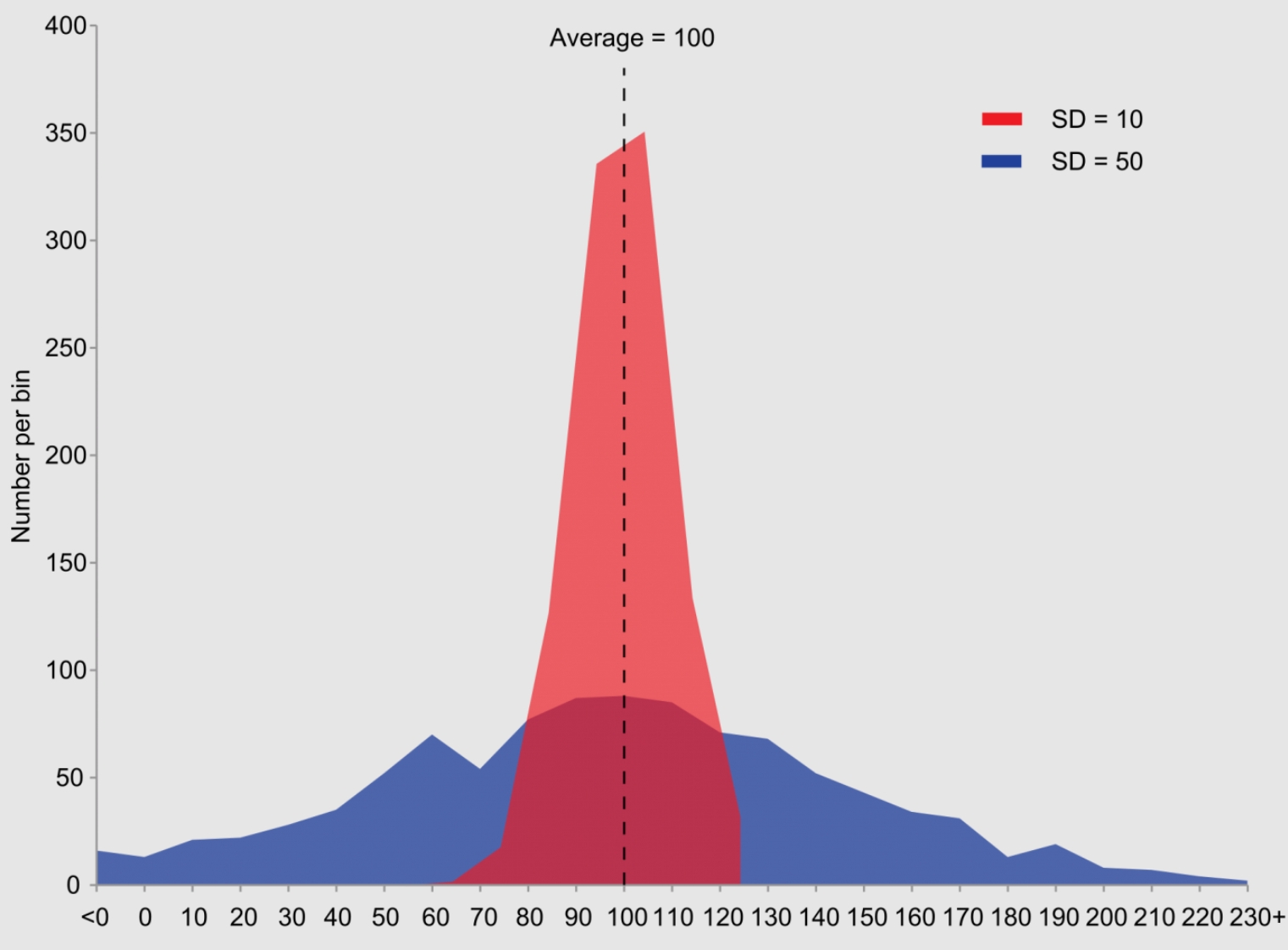
1. 平均は同じであるが標準偏差が大きく異なるデータのヒストグラムの例。
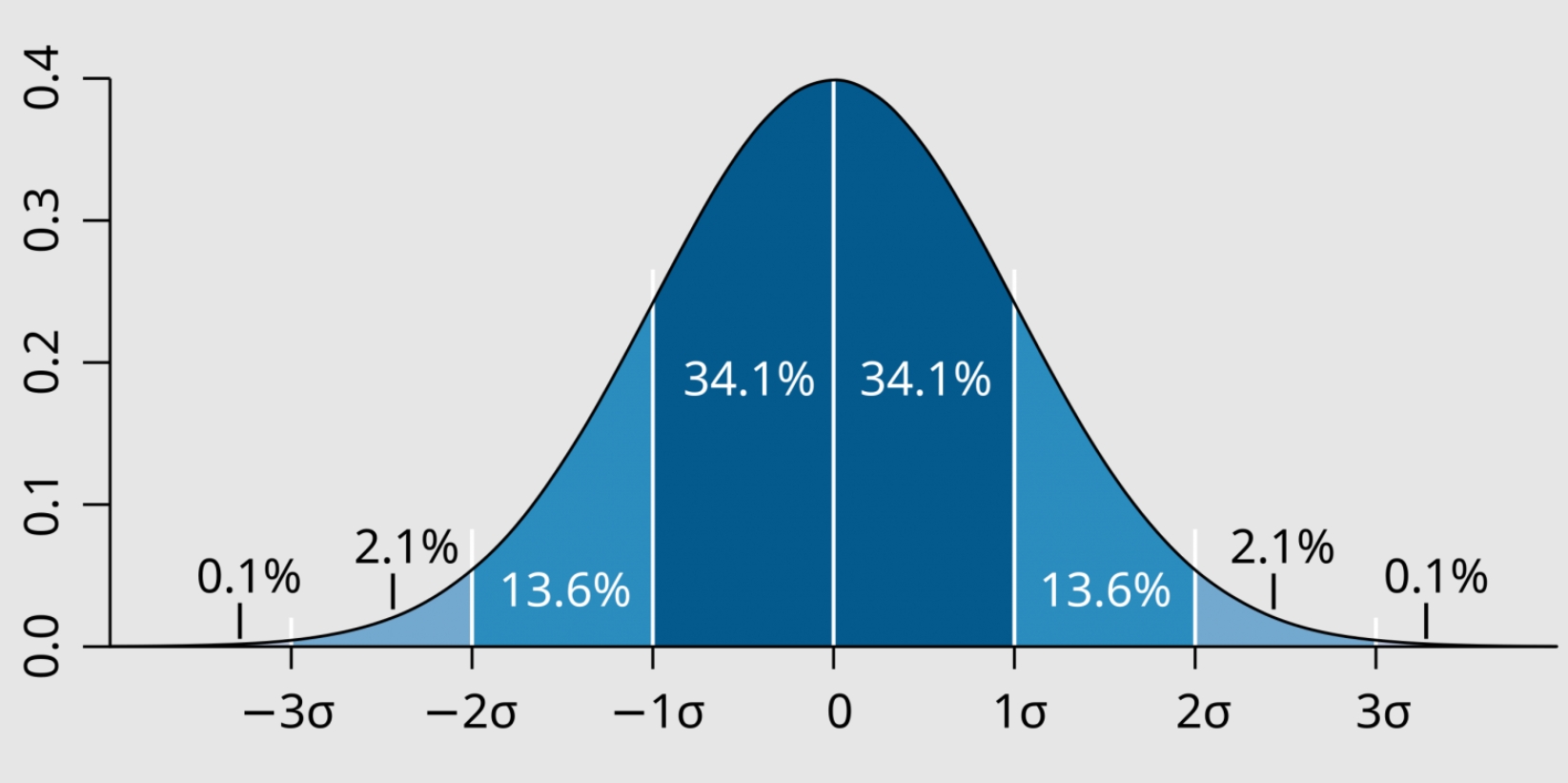
2. 平均 0, 標準偏差 σ の正規分布の確率密度関数。
関連記事
参考リンク
https://ja.wikipedia.org/wiki/%E6%A8%99%E6%BA%96%E5%81%8F%E5%B7%AE